40多年的策动机贫窭——劳作海狸贫窭好看的第四色，被一群业余把稳者攻破了！

数学大佬陶哲轩转发了这一音信，并痛快默示：

这再一次体现了证明助手关于数学盘考的调和是何等灵验。

策动机科学家Scott Aaronson为此还写了一篇博文，并鼎力维持：

这个发现是自1983年以来，劳作海狸函数盘考取最要紧的阐发。

具体而言，东说念主们历经数十年悉力，终于找到了第五个“劳作海狸”图灵机：

BB(5) =47，176，870（5状况图灵机，能在停驻来之前写下47，176，870个“1”）

图灵机是一种轮廓的策动模子，通过读取和写入0和1在无尽磁带上进行策动。

早在40多年前，一群策动机科学家在德国多特蒙德举行竞赛，寻找“劳作海狸”图灵机。

性吧有你

找出一个特定的图灵机，在它罢手之前大约写下最多的1（咱们称之为劳作海狸数）。

通过找出特定状况下能在罢手前写下最多1的图灵机，咱们能更好地厚实策动表面的范围。

自从1974年细则了第四个劳作海狸数后，寻找第五个成了悬而未决的问题。

而面前，来自全国各地的20多名孝顺者（其中大多数东说念主莫得传统的学术阅历） ，使用一款名为Coq证明助手的软件获取了限制——47，176，870，该软件证实数学证明莫得作假。

这一设立眨眼间令社区怡悦，其中爱尔兰梅努斯大学策动机科学家Damien Woods感叹：

就像博尔特相似，我很骇怪他们的速率如斯之快！

嗯，快半个世纪往时了还算快？只能说这个问题雀食有亿点难。

别慌张，且看这群东说念主如何长江后浪催前浪收拢“第5只海狸”~

为什么提议“劳作海狸”？

要回应这个问题，发轫需要肤浅了解一下二进制图灵机。

1936年，策动机科学之父艾伦·图灵提议了图灵机——

由一个无尽长的纸带，一个读写头（不错读取和写入纸带上的信息），以及一组里面状况等基本部分构成。

图灵机的行径由一组法规界说，这些法规不错念念象成一张表。表中的每行代表一个法规，每列对应读写头读取到的记号（0或1）。

每条法规指定了在特定状况下，读写头遭逢0或1时应该扩充的操作。操作频繁包括：

写入记号：决定在刻下单位格写入什么记号（举例，将0替换为1）。

移动标的：决定读写头是向左移动、向右移动如故保抓不动。

状况蜕变：决定图灵机的下一个状况是什么。

除了处理0和1的法规外，还有一条非凡法规告诉图灵机何时罢手运行。当图灵机干预这个状况时，它就不再扩充当何操作，相等于“比赛实现”（这种状况一般不策动在状况结合里）。

而就在停机问题上，也曾有盘考不雅察到：

一些图灵契机相对较快地罢手（比如这台three-rule图灵机在11步后罢手）

灵通新闻客户端 提高3倍陶冶度

其他的则堕入了很容易发现的无尽轮回

灵通新闻客户端 提高3倍陶冶度

这也启发图灵提议了有名的“停机问题”：

图灵机是否会在有限的才调后罢手运行，或者它是否会无尽期地运行下去？

他还进一步提到，停机问题莫得通用的惩办决议，因为东说念主们永恒无法细则适用于一台机器的步调是否也适用于另一台机器。

关于这个论断，数学家Tibor Radó（以下简称拉多）不太酣畅，并由此发明了“劳作的海狸游戏”。

为了将停机问题的内容索取成更肤浅的样子，拉多提议了一种步调——

将图灵机凭证它们领有的法规数目进行分组。

举例，一组代表所有这个词唯有一条法规的图灵机，另一组代表所有这个词有两条法规的图灵机，以此类推。

1962年，拉多应用这些有限的图灵机组界说了“劳作海狸游戏”。游戏的玩法是：

1.剿袭一个组，即细则你的图灵机将领有的法规数目。

2.为组中的每台机器提供一个运转状况全是0的磁带。

3.不雅察这些机器的运行。一些机器可能会无尽期地运行下去，而其他的则会在某个时刻罢手。

4.在那些最终罢手的机器中，有的会很快罢手，有的则需要更多才调。每个组中会有一个运行时刻最长的机器，这台机器被称为“劳作海狸”。

5.在有n条法规的组中，这台“劳作海狸”在罢手之前所扩充的步数便是所谓的“劳作海狸数”BB(n)。

6.游戏的指标是细则这些BB(n)果真凿值。

拉多给这么“至极低效”的图灵机取了一个真谛真谛且形象的名字：劳作海狸（Busy Beaver，取自英语中的成语 as busy as a beaver）。

而这个游戏也最终引来一众轨范员和数学把稳者的苟且试玩。

早期吃螃蟹的东说念主

Allen Brady（以下简称布雷迪），那时的俄勒冈州立大学数学盘考生，成了早期挑战者之一。

在游戏推出前，东说念主们也曾细则了BB(1) = 1，BB(2) = 6，那时东说念主们正尝试攻克BB(3)。

布雷迪也投身BB(3)，他编写了策动机轨范来模拟图灵机的行径，这个轨范构建了一种“家支”，凭证图灵机运转行径的相似性，对具有疏通法规数目的机器进行分类。

轨范只在机器之间行径相反变得要紧时才将家支树分红多个分支。若是模拟败露某条分支上的机器会罢手或干预无尽轮回，轨范就会剪掉这个分支，抛弃那些不会无尽运行下去的图灵机。

编写轨范仅仅第一步，布雷迪需要找到阔气雄伟的策动机来运行它。

在1964年，这不是一件容易的事。最终，他在90英里外的灵长类动物盘考施行室找到了一台SDS 920策动机。

只能惜BB(3)进行到一半，拉多的盘考生Shen Lin已晓谕证明BB(3) = 21，不外布雷迪如故陆续证实了Lin的限制。

毕业后，布雷迪发现了新的非罢手图灵机种类，并给它们起了形象的名字。

1966年，他发现了一个在罢手前运行了107步的四法规图灵机，并猜想这可能是第四个劳作海狸，并最终于1974年证明了莫得其他罢手的机器能运行更久。

这是四十多年来东说念主类所知的临了一个劳作的海狸号码

1982年，第一次大鸿沟寻找BB(5)）的Dortmund竞赛负责举办，其中运行时刻最长的一台在跳跃10万步后罢手。

1984年，《科学好意思国东说念主》对这项比赛的报说念激勉了新一代盘考者的酷好，有一位盘考者冲突了旧记录，他发现的一台机器在跳跃200万步后罢手。

这一新记录也引来那时的盘考生Heiner Marxen和 Jürgen Buntrock，他们在业余时刻合作盘考这个问题，成立了加快图灵机模拟的数学技巧。

尽管未能冲突200万步的记录，但其后在1989年，Marxen在一家公司责任时，使用一台功能雄伟的新策动机再行启动了他的搜索轨范，并无意地发现了一个在4700万步后罢手的图灵机。

2000年代初，一位名叫Georgi Ivanov Georgiev（假名Skelet）的保加利亚策动机科学家卓著接近这一指标。

经由两年的不懈悉力，他成立了一个大约识别非罢手机器新种类的策动机轨范。尽管他的轨范运行了一周并留住了约100个未惩办的图灵机，但他手工分析后将名单减少到43个。

尔后东说念主们一直堕入不停尝试中。

最终细则BB(5)

2022年，盘考生Tristan Stérin发起了“劳作海狸挑战”，这是一项在线合作，旨在最终细则BB(5)。

在这之前，Stérin决定在传统步调的基础上进行养息，使用布雷迪的家支步调，并筹划用寂寥轨范处理永恒运行的机器。

到2021年底，Stérin编写了第一步的策动机轨范，生成了约莫1.2亿台可能的图灵机列表。

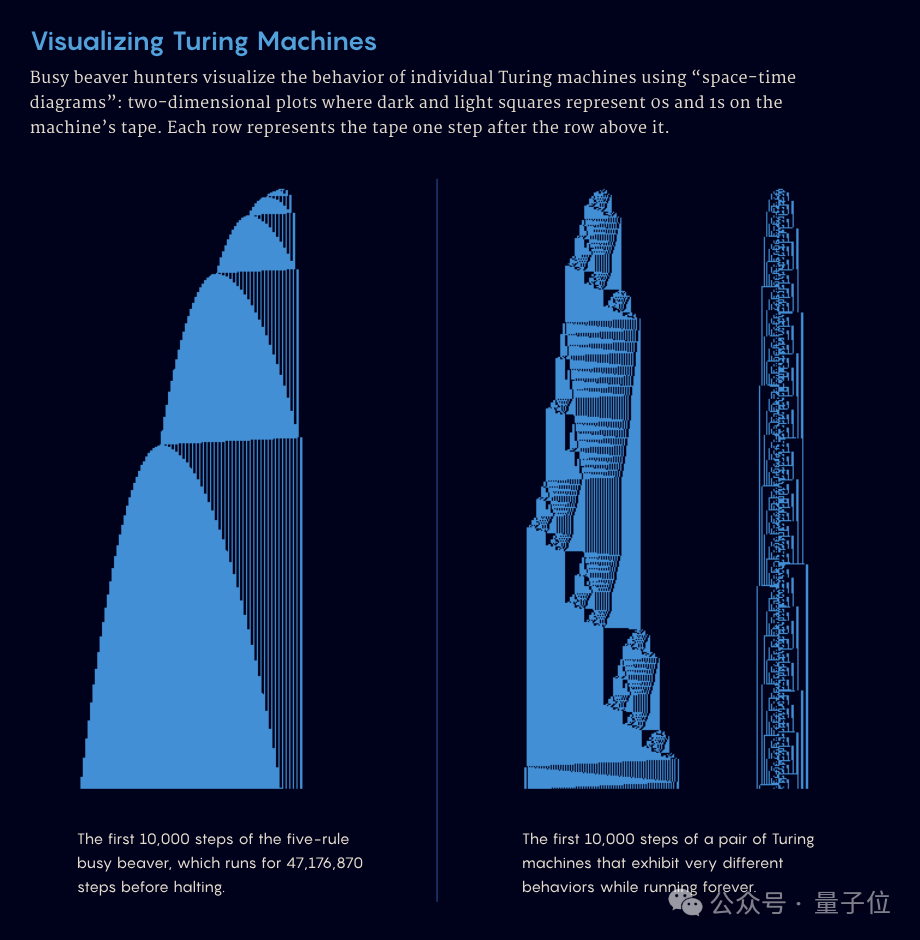
为了匡助分析这些机器，Stérin构建了一个在线界面，使用“时空图”来可视化图灵机的行径。

完成这些后，鉴于个东说念主元气心灵有限，他在只怕的情况下拉来了Shawn Ligocki。

Ligocki向团队先容了闭塞磁带谈话步调，这是一种30年前的技巧，他将其应用于刻下的劳作海狸问题。

他写了一篇博客著述先容这项技巧，但率先并不知说念如何编写一个能涵盖所有这个词情况的轨范。

然后，又一位Justin Blanchard加入了神志，他念念出了如何作念到这极少，但他的轨范相对徐徐。

于是另外两个孝顺者找到了让它运行得更快的步调，这一技巧以至不错处理前文提到的43个未惩办图灵机中的10个。

取得阶段性后果后，BB(5)终于迎来两个要津突破。

第一个是Skelet #1，它在可展望行径和错杂行径之间不拒却替，这种特点使得它卓著难以分析和厚实。

2023年3月，Ligocki和斯洛伐克孝顺者Pavel Kropitz（不会说英语，使用谷歌翻译与团队其他成员交流），使用Marxen和Buntrock（之前挑战200万步记录的两位学生）30年前的加快模拟技巧的一个增强版，最终破解了Skelet #1。

他们发现Skelet #1在跳跃一万亿步之后才干预一个特殊长的肖似周期，远跳跃一般无尽轮回在1，000步内入手肖似的通例。

由于Skelet #1的行径极其奇怪，Ligocki在快要五个月的时刻里皆不细则他们的证明限制是否正确。

其后，一位21岁自学成才的轨范员（以“mei”为名）加入了团队，她通过学习Coq证明助手，将团队的一些证明翻译成Coq谈话，提高了证明的严格性和可靠性。

第二个突破是Skelet #17，盘考者必须像破译四层加密的深奥音信相似，逐层理解其行径方式，才调证明该机器永恒不会罢手。

尽管盘考生Chris Xu和其他社区孝顺者作念了多半责任，但大多数证明尚未翻译成Coq。

直到2023年4月，一位名为mxdys的深奥新孝顺者加入，并在短短几周内完成了一个40，000行的Coq证明，证实了BB(5) 的值。

mxdys证明第五台劳作海狸在4700万步后罢手，阐发了Marxen和Buntrock的发现。

Coq群众Yannick Forster审查了证明，他慷慨默示：

我仍然感到卓著畏怯。

故事仍未实现

BB(5)终于阐发了，面前有关盘考者正在草拟一份学术论文，这将是一个补充mxdys的Coq证明的东说念主类可读版块。

可是，BB(5)已阐发，BB(6)还会远吗？

mxdys和另一位孝顺者Racheline发现了一个六法规的图灵机，其停机问题与有名的数学贫窭“科拉茨猜念念”相似。

为了幸免让群众头疼，此处不再伸开这个猜念念，列位看官只需要知说念它卓著难就行。

以至于有名表面策动机科学家Scott Aaronson发出感慨：

BB(5)也许是咱们所知说念的临了一个劳作的海狸号码

嗯？这话有点耳熟，BB(4)好像亦然这么说的。

— 完 —好看的第四色